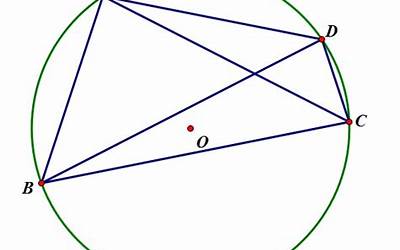
四点共圆问题是解析几何中经典的问题,在解析几何中研究了几何图形的特殊性质。证明四点共圆的方法有很多,比如向量方法、坐标法、轮廓线等方法,下面我们将分别详细介绍。
一、向量法。
设四个点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则向量AB=(x2-x1,y2-y1),向量AC=(x3-x1,y3-y1),向量AD=(x4-x1,y4-y1),则四点共圆等价于。
(AB,AC) = (AB,AD)。
即向量AB和向量AC的夹角等于向量AB和向量AD的夹角。向量夹角公式为。
cosθ=(u,v)/(|u||v|)。
其中(u,v)表示向量u和v的点积,|u|和|v|分别表示向量u和v的模长。则。
(AB,AC) = cos(θAC-θAB) = ((x3-x1)(x2-x1)+(y3-y1)(y2-y1))/sqrt((x3-x1)²+(y3-y1)²)/sqrt((x2-x1)²+(y2-y1)²)。
(AB,AD) = cos(θAD-θAB) = ((x4-x1)(x2-x1)+(y4-y1)(y2-y1))/sqrt((x4-x1)²+(y4-y1)²)/sqrt((x2-x1)²+(y2-y1)²)。
如果(AB,AC) = (AB,AD),则四点共圆。
二、坐标法。
设四个点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则四点共圆等价于。
(x1-a)²+(y1-b)²=(x2-a)²+(y2-b)²=(x3-a)²+(y3-b)²=(x4-a)²+(y4-b)²。
其中(a,b)为圆心坐标。展开得到。
x1²+y1²-2ax1-2by1+a²+b² = x2²+y2²-2ax2-2by2+a²+b² = x3²+y3²-2ax3-2by3+a²+b² = x4²+y4²-2ax4-2by4+a²+b²。
将其中三个式子相减,得到。
2a(x1-x2)(y3-y1)+2b(y1-y2)(y3-y1)=x1²+y1²-x2²-y2²+x3²+y3²-x4²-y4²。
同理将其中三个式子相减,得到。
2a(x1-x2)(y4-y1)+2b(y1-y2)(y4-y1)=x1²+y1²-x2²-y2²+x4²+y4²-x3²-y3²。
解这个方程组,求出a和b,即可得到圆心坐标。然后将圆心坐标代入其中一个式子中,判断四个点是否共圆。
三、轮廓线法。
轮廓线是指由两个圆的半径和距离组成的一条直线。对于四点共圆的问题,我们可以通过构造轮廓线的方法来证明。
设四个点A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则轮廓线表示为。
r1+r2=d1。
r1+r3=d2。
r1+r4=d3。
其中ri为第i个点到圆心的距离,di为第i个点和其他三个点之间的距离。将上面三个式子展开,得到。
r1=(d1+d2+d3)/2-sqrt((d1+d2+d3)²/4-d1d2-d1d3-d2d3)/2。
r2=d1-r1。
r3=d2-r1。
r4=d3-r1。
然后计算出四个点到圆心的距离ri,判断是否满足上面的式子,即可判断四点是否共圆。这种方法的好处是不需要求解方程组,计算量较小,适合快速判断四点共圆的问题。
综上所述,证明四点共圆的方法有很多种,可以根据具体情况选择合适的方法。对于初学者来说,建议从向量法入手,逐步掌握其他方法。
如何证四点共圆
四点共圆可以用以下两种方法证明:。1. 应用圆的定义:如果一个点到另外两个点的距离相等,那么这三个点就在同一条直线上;如果一个点到另外三个点的距离相等,那么这四个点就在同一个圆上。因此,如果要证明四个点共圆,只需要证明其中任意三个点的距离相等即可。具体证明步骤如下:。- 假设四个点分别为A、B、C、D,且它们在同一平面上。- 连接任意两点,得到线段AB、AC、AD、BC、BD、CD。- 计算线段AB、AC、AD的长度,判断它们是否相等。- 如果相等,则说明A、B、C三个点在同一圆上,接下来只需要计算线段BC和BD与已知长度是否相等即可。- 如果不相等,则考虑另外三个点,重复以上步骤即可。2. 应用圆的性质:圆的性质包括切线垂直于半径、向心角等于弧角的一半、圆弧上的任意角都相等等。因此,可以通过观察四个点所在的图形是否具有圆的性质来证明它们共圆。具体证明步骤如下:。- 观察四个点所在的图形,判断它们是否具有圆的性质。- 如果具有,则说明这四个点在同一个圆上。- 如果不具有,则需要用其他方法继续证明。需要注意的是,以上两种方法只是证明四点共圆的常见方法,有些情况下可能需要用其他方法。此外,在实际问题中,还需要注意误差和精度的影响,以确保证明的正确性。
怎么证四点共圆
证明四点共圆的方法主要有以下两种:。1. 利用圆的性质进行推导。若四点共圆,可以通过圆的性质推导出它们共圆。比如,四点共圆可以等价于它们构成的任意三角形外接圆过三点,四点所在直线的垂线交于同一点等。2. 利用向量或坐标几何进行计算。若已知四个点的坐标或向量,则可以通过计算它们之间的距离、夹角等来证明它们共圆。比如,当四个点在同一平面上时,它们共圆可以等价于它们构成的两个向量的叉积为零,或者通过计算它们到某一定点的距离是否相等来进行证明。
数你好看四点共圆
有不同的方法可以证明四点共圆,以下介绍其中几种方法:。1. 通过欧拉定理证明四点共圆。欧拉定理指出,对于一个三角形ABC及其外接圆O,点H为三角形的垂心(垂足连线的交点),则点O、H、A、B、C五点共圆。所以,如果给定四个点A、B、C、D,我们可以构造一个三角形ABC(点D不在三角形内),然后求出三角形的垂心H,如果点D也在同一条垂线上,那么就证明四点共圆了。2. 通过中垂线相交定理证明四点共圆。中垂线相交定理指出,如果一个四边形ABCD的对角线AC和BD的中垂线相交于点O,则该四边形的四个顶点A、B、C、D共圆。因为对于任意一条弦,它的中垂线恰好垂直于这条弦,所以如果四个点在同一圆上,那么它们组成的四边形的对角线的中垂线肯定相交于同一点。3. 通过面积相等证明四点共圆。如果一个四边形的四个顶点共圆,则它们的对角线互相垂直,而且对角线的交点是四边形的中心。如果我们可以证明这个四边形的两个对角线互相垂直,并且任意两个三角形的面积之和相等,那么就可以证明这四个点共圆。4. 通过勾股定理证明四点共圆。如果一个四边形的四个顶点共圆,则它们的对角线互相垂直,而且对角线的交点是四边形的中心。如果我们可以证明这个四边形的任意两个相邻边的长度之和的平方等于另外两边长度之和的平方,那么就可以证明这四个点共圆。
证明四点共圆的方法
证明四点共圆,需要证明它们在同一个圆上。下面是两种方法:。方法一:使用圆的性质。1. 设四点分别为A、B、C、D,它们的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)。2. 计算出AB、AC、AD三条线段的斜率。3. 判断AB、AC、AD三条线段是否相互垂直,如果是,则四点共圆。4. 如果AB、AC、AD三条线段不相互垂直,则计算出它们的垂线的交点P。5. 计算出AP的长度和BP、CP、DP的长度,如果它们相等,则四点共圆。方法二:使用勾股定理。1. 设四点分别为A、B、C、D,它们的坐标分别为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)。2. 计算出AB、AC、AD三条线段的长度。3. 若AB=BC+CD,则四点共圆;若不成立,则四点不共圆。4. 如果AB、AC、AD的长度不满足勾股定理,可以将它们的平方作为数列,使用高斯消元等方式求解,如果存在解,则四点共圆。注意:以上两种方法都是用于判断四点是否共圆。如果需要证明四点共圆,则需要使用更为复杂的几何证明方法,例如使用圆形相似定理、共圆角定理等。