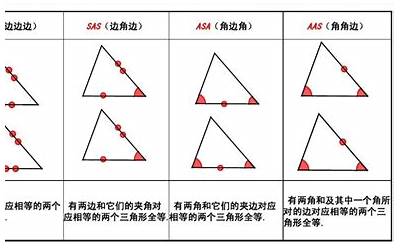
三角形是初中数学中的重要内容,它是平面几何中最基本、最常见的图形之一。在三角形的研究中,三角形的全等关系是重要的一个概念。接下来,本文将重点介绍证明全等三角形的五种方法。
一、SSS 判定法。
SSS 判定法是指如果两个三角形的三条边分别相等,则这两个三角形全等。
证明过程如下:。
已知:△ABC ≌ △DEF(其中“≌”表示两个三角形全等)。
证明:AB = DE, BC = EF, AC = DF。
由全等三角形的定义可知,△ABC 和 △DEF 对应的三条边分别相等,即 AB = DE, BC = EF, AC = DF。
因此,根据 SSS 判定法,可以得出 △ABC ≌ △DEF。
二、SAS 判定法。
SAS 判定法是指如果两个三角形的两边和夹角分别相等,则这两个三角形全等。
证明过程如下:。
已知:△ABC ≌ △DEF(其中“≌”表示两个三角形全等)。
证明:AB = DE, BC = EF, ∠BAC = ∠EDF。
由全等三角形的定义可知,△ABC 和 △DEF 对应的三条边分别相等,即 AB = DE, BC = EF。
又因为根据全等三角形的定义,对应角相等,则∠BAC = ∠EDF。
因此,根据 SAS 判定法,可以得出 △ABC ≌ △DEF。
三、ASA 判定法。
ASA 判定法是指如果两个三角形的两个角和夹边分别相等,则这两个三角形全等。
证明过程如下:。
已知:△ABC ≌ △DEF(其中“≌”表示两个三角形全等)。
证明:∠BAC = ∠EDF, ∠ABC = ∠DEF, AC = DF。
由全等三角形的定义可知,△ABC 和 △DEF 对应的三条边分别相等,即 AB = DE, BC = EF, AC = DF。
又因为根据全等三角形的定义,对应角相等,则∠BAC = ∠EDF, ∠ABC = ∠DEF。
因此,根据 ASA 判定法,可以得出 △ABC ≌ △DEF。
四、HL 判定法。
HL 判定法是指如果两个三角形的一条斜边和与其相邻的两个角分别相等,则这两个三角形全等。
证明过程如下:。
已知:△ABC ≌ △DEF(其中“≌”表示两个三角形全等)。
证明:AC = DF, ∠BAC = ∠EDF, ∠ABC = ∠DEF。
由全等三角形的定义可知,△ABC 和 △DEF 对应的三条边分别相等,即 AB = DE, BC = EF, AC = DF。
又因为根据全等三角形的定义,对应角相等,则∠BAC = ∠EDF, ∠ABC = ∠DEF。
因此,根据 HL 判定法,可以得出 △ABC ≌ △DEF。
五、RHS 判定法。
RHS 判定法是指如果两个三角形的一条直角边和另外一条边以及它们的对应边分别相等,则这两个三角形全等。
证明过程如下:。
已知:△ABC ≌ △DEF(其中“≌”表示两个三角形全等)。
证明:AB = DE, BC = EF, ∠BAC = ∠EDF。
由全等三角形的定义可知,△ABC 和 △DEF 对应的三条边分别相等,即 AB = DE, BC = EF, AC = DF。
又因为根据全等三角形的定义,对应角相等,则∠BAC = ∠EDF。
因此,根据 RHS 判定法,可以得出 △ABC ≌ △DEF。
综上所述,









